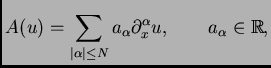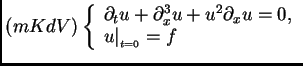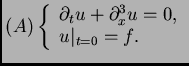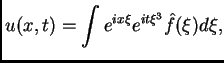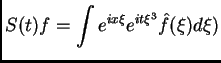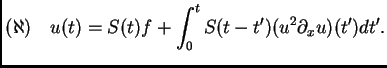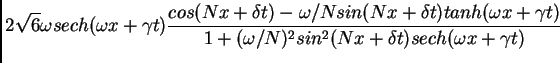Análisis Armónico y Ecuaciones Diferenciales Dispersivas
Carlos Kenig
Carlos Kenig: Math. Dept, University of Chicago, Chicago, Il. 60637, USA
cek@math.uchicago.edu
El análisis armónico y las ecuaciones en derivadas parciales
han estado entrelazados desde sus comienzos, en la obra de Joseph
Fourier (1768-1830). En su famoso estudio de la teoría
matemática de conducción del calor (1807), Fourier dedujo una
ecuación (la ecuación del calor) para describir el flujo de
calor en una barra unidimensional, a partir de la ``Ley de
enfriamiento de Newton" (el flujo de calor a través de un punto
es proporcional al gradiente temperatura en ese punto).
La ecuación es
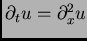 , y Fourier
resolvió el ``problema a valores iniciales" (PVI) para esta
ecuación, es decir dada la temperatura inicial de una barra
finita, cuyos extremos son mantenidos a temperatura constante,
Fourier calculó la temperatura en el futuro, en cualquier punto
de la barra. En el curso del cálculo de la solución, Fourier
hizo una afirmación, que ha motivado el estudio del Análisis
Armónico desde ese momento. La afirmación de Fourier fue la
siguiente:
Cualquier función
, y Fourier
resolvió el ``problema a valores iniciales" (PVI) para esta
ecuación, es decir dada la temperatura inicial de una barra
finita, cuyos extremos son mantenidos a temperatura constante,
Fourier calculó la temperatura en el futuro, en cualquier punto
de la barra. En el curso del cálculo de la solución, Fourier
hizo una afirmación, que ha motivado el estudio del Análisis
Armónico desde ese momento. La afirmación de Fourier fue la
siguiente:
Cualquier función 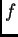 , definida en [-
, definida en [-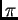 ,
, 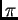 ], sin
importar cuán caprichoso sea su gráfico, puede ser representada
como una suma infinita de funciones trigonométricas:
], sin
importar cuán caprichoso sea su gráfico, puede ser representada
como una suma infinita de funciones trigonométricas:
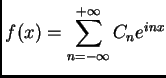
Más aún, Fourier dio una receta para calcular 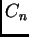 :
:
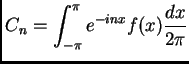
Esta afirmación fue muy controvertida, porque
 son
funciones ``buenas", y entonces cómo puede ser posible que
funciones ``malas" puedan ser representadas por su suma. Todaví
a hoy se sigue estudiando esta cuestión.
Aún cuando la afirmación de Fourier es falsa para todas las
funciones y todos los puntos
son
funciones ``buenas", y entonces cómo puede ser posible que
funciones ``malas" puedan ser representadas por su suma. Todaví
a hoy se sigue estudiando esta cuestión.
Aún cuando la afirmación de Fourier es falsa para todas las
funciones y todos los puntos  , el método de Fourier
funcionó, y rápidamente tuvo un número de importantes
aplicaciones. Por ejemplo:
El cálculo de la temperatura de la tierra. La predicción de
las mareas (Kelvin). El ``analista armónico" (una máquina). El
cable transatlántico (Kelvin). El cálculo de la edad de la
tierra, etc..
Cuando se estudia el flujo de calor en una barra infinita (Fourier
1822) uno es llevado a estudiar representaciones análogas para
funciones, como integrales, de la forma
, el método de Fourier
funcionó, y rápidamente tuvo un número de importantes
aplicaciones. Por ejemplo:
El cálculo de la temperatura de la tierra. La predicción de
las mareas (Kelvin). El ``analista armónico" (una máquina). El
cable transatlántico (Kelvin). El cálculo de la edad de la
tierra, etc..
Cuando se estudia el flujo de calor en una barra infinita (Fourier
1822) uno es llevado a estudiar representaciones análogas para
funciones, como integrales, de la forma
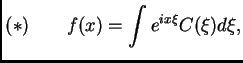
donde la fórmula de 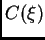 debe ser
debe ser
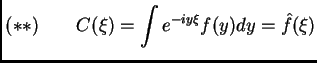
El hecho que (*) es cierta para muchas funciones, en
sentidos apropiados, ha sido instrumental en el estudio de
las ecuaciones en derivadas parciales lineales (de las cuales la
ecuación del calor es un ejemplo), en los últimos 100 años.
La idea básica de Fourier para el (PVI) para la ecuación del
calor es que, si lo resolvemos para
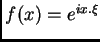 , para cada
, para cada
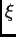 , (*) y linealidad nos dan la solución general. Esto se
extiende a dimensiones mayores
, (*) y linealidad nos dan la solución general. Esto se
extiende a dimensiones mayores
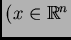 ), y ha sido
instrumental en el desarrollo espectacular de las ecuaciones
lineales en derivadas parciales, en el siglo 20.
Volviendo a (*), (**) una posible manera de darle significado es
preguntarse si (o cuándo) se tiene
), y ha sido
instrumental en el desarrollo espectacular de las ecuaciones
lineales en derivadas parciales, en el siglo 20.
Volviendo a (*), (**) una posible manera de darle significado es
preguntarse si (o cuándo) se tiene
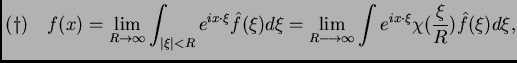
donde
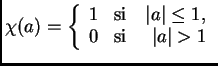
Observen que
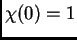 . Una conjetura famosa del matemático
ruso Lusin
. Una conjetura famosa del matemático
ruso Lusin
 era que
era que  es cierta para toda
es cierta para toda
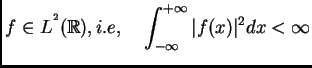
y casi todo 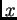 , (en el sentido de la medida de
Lebesgue). Esta conjetura, para
, (en el sentido de la medida de
Lebesgue). Esta conjetura, para  fue probada por L. Carleson
en 1966, quien lo hizo de mostrando la siguiente desigualdad:
fue probada por L. Carleson
en 1966, quien lo hizo de mostrando la siguiente desigualdad:
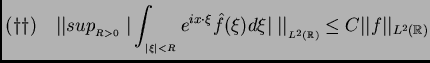
La necesidad de una estimación del tipo (**) para la validez de
la conjetura de Lusin había sido establecida previamente, por
A. P. Calderón. Ahora nos vamos a concentrar en una familia de
ecuaciones diferenciales parciales no lineales, para las cuales se
ha usado, con mucho éxito las ideas del análisis armónico. Estas son
las llamadas ``ecuaciones dispersivas no-lineales'', que aparecen
como modelos en algunos problemas de propagación de ondas. El
ejemplo en el que me voy a enfocar es la familia de (PVI):
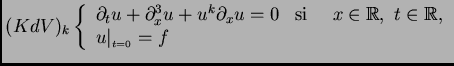
El caso 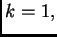 usualmente llamado KdV aparece en el estudio de la
propagación de olas en canales poco profundos. El caso
usualmente llamado KdV aparece en el estudio de la
propagación de olas en canales poco profundos. El caso 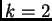 (usualmente llamado mKdV) es importante porque muchos modelos
hiperbólicos se reducen a mKdV. Estos dos casos también son de
particular importancia porque el método de ``inverse scattering"
se les aplica, para obtener soluciones. Hablaremos más de esto
luego. Hemos decidido ilustrar las ideas concentrándonos en mKdV,
el caso
(usualmente llamado mKdV) es importante porque muchos modelos
hiperbólicos se reducen a mKdV. Estos dos casos también son de
particular importancia porque el método de ``inverse scattering"
se les aplica, para obtener soluciones. Hablaremos más de esto
luego. Hemos decidido ilustrar las ideas concentrándonos en mKdV,
el caso 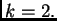 Debemos primero desarrollar terminología, inspirada
por la teoría de ecuaciones diferenciales ordinarias. Consideremos
un problema a valores iniciales (PVI)
Debemos primero desarrollar terminología, inspirada
por la teoría de ecuaciones diferenciales ordinarias. Consideremos
un problema a valores iniciales (PVI)
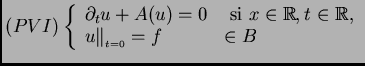
donde 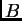 es un espacio funcional, y
es un espacio funcional, y 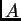 es un operador
diferencial (posiblemente no lineal) en las variables espaciales
es un operador
diferencial (posiblemente no lineal) en las variables espaciales
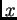 , actuando (apropiadamente) sobre funciones en
, actuando (apropiadamente) sobre funciones en 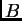 . Para mKdV,
. Para mKdV,
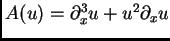 . Decimos que el
. Decimos que el 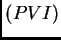 está globalmente bien propuesto en
está globalmente bien propuesto en 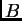 (gbp), si dada
(gbp), si dada 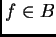 ,
existe una única
,
existe una única
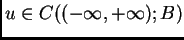 , que resuelva
, que resuelva
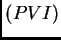 (en un sentido adecuado) y tal que la aplicación
(en un sentido adecuado) y tal que la aplicación
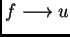 es continua. Si esto se satisface con el
intervalo de tiempo
es continua. Si esto se satisface con el
intervalo de tiempo
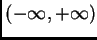 reemplazado por el
reemplazado por el
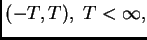 decimos que
decimos que 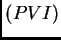 está localmente bien
propuesto en
está localmente bien
propuesto en 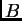 (lbp). Aquí estamos considerando intervalos de
tiempo que son simétricos alrededor de
(lbp). Aquí estamos considerando intervalos de
tiempo que son simétricos alrededor de 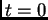 , porque los problemas
que estamos considerando son reversibles en tiempo. Para mKdV,
, porque los problemas
que estamos considerando son reversibles en tiempo. Para mKdV, 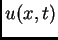 es
solución si y sólo si
es
solución si y sólo si
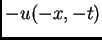 es solución. Esto, por supuesto
no es cierto para la ecuación del calor que discutimos antes, y
uno toma entonces intervalos de la forma
es solución. Esto, por supuesto
no es cierto para la ecuación del calor que discutimos antes, y
uno toma entonces intervalos de la forma 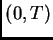 . Dado un
. Dado un 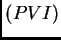 ,
una de las preguntas más básicas es ¿Para cuáles espacios
,
una de las preguntas más básicas es ¿Para cuáles espacios 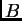 tenemos (lbp), (gbp)?. Aquí nos limitaremos a considerar la escala
de espacios de Sobolev
tenemos (lbp), (gbp)?. Aquí nos limitaremos a considerar la escala
de espacios de Sobolev
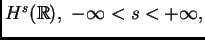 de
funciones que tienen
de
funciones que tienen 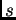 derivadas en
derivadas en
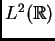 . Rigurosamente:
. Rigurosamente:
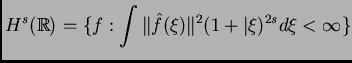
Esto se justifica porque
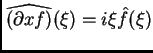 .
Nuestra pregunta entonces es:
¿Para cuáles
.
Nuestra pregunta entonces es:
¿Para cuáles 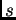 es mKdV
es mKdV
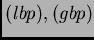 en
en
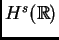 ?
Observen que, para un problema de evolución lineal, a coeficientes
constantes, esto es cuando
?
Observen que, para un problema de evolución lineal, a coeficientes
constantes, esto es cuando
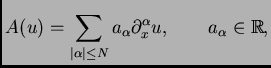
la pregunta no tiene interés, ya que
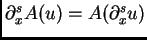 , y por eso el correspondiente
, y por eso el correspondiente 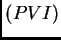 está
(lbp) para un
está
(lbp) para un 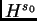 sí y solo sí lo está para todo
sí y solo sí lo está para todo 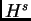 .
Vemos, de esta manera, que la pregunta está relacionada con la
interacción entre las partes lineales y no lineales de
.
Vemos, de esta manera, que la pregunta está relacionada con la
interacción entre las partes lineales y no lineales de 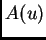 .
Para mKdV, estas son
.
Para mKdV, estas son
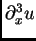 y
y
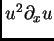 , respectivamente.
Para explicar cómo el análisis armónico juega un papel en entender
esta pregunta, volvamos al teorema de Carleson, que dice que, para
toda
, respectivamente.
Para explicar cómo el análisis armónico juega un papel en entender
esta pregunta, volvamos al teorema de Carleson, que dice que, para
toda
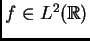 , y casi todo
, y casi todo 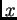 , tenemos
, tenemos
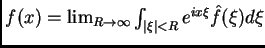
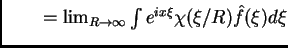
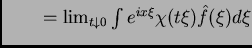 ,
y recordando que
,
y recordando que
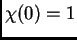 , vemos que esto nos da la
'inversión de Fourier'.
En los años 70, en conexión con sus trabajos en mecánica
estadística, Carleson se vio forzado a considerar preguntas
análogas, cuando
, vemos que esto nos da la
'inversión de Fourier'.
En los años 70, en conexión con sus trabajos en mecánica
estadística, Carleson se vio forzado a considerar preguntas
análogas, cuando 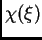 es `oscilatoria'. Un ejemplo es el
caso
es `oscilatoria'. Un ejemplo es el
caso
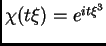 , y la pregunta de Carleson, en
este caso es: ¿Tenemos, para
, y la pregunta de Carleson, en
este caso es: ¿Tenemos, para
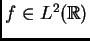
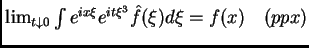 ?
Carleson mostró que la respuesta es NO, pero que si
?
Carleson mostró que la respuesta es NO, pero que si 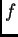 tiene ``un
poco" más de regularidad, (precisamente cuando
tiene ``un
poco" más de regularidad, (precisamente cuando 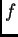 tiene 1/4 de
derivada en
tiene 1/4 de
derivada en
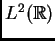 ), o más formalmente, cuando
), o más formalmente, cuando
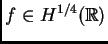 , la respuesta es SI. Luego, B. Dahlberg y yo nos
interesamos en esta pregunta, y demostramos (1979), que para
, la respuesta es SI. Luego, B. Dahlberg y yo nos
interesamos en esta pregunta, y demostramos (1979), que para
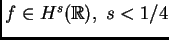 , en general la respuesta es NO, es decir
el resultado de Carleson es óptimo. ¿Cuál es la relación entre
éste y el problema
, en general la respuesta es NO, es decir
el resultado de Carleson es óptimo. ¿Cuál es la relación entre
éste y el problema 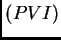 para mKdV?
para mKdV?
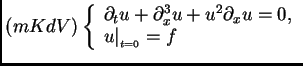
Como lo mencionamos antes, la pregunta sobre (lbp), (gbp) tiene
que ver con la interacción entre
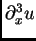 (parte lineal) y
(parte lineal) y
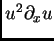 (parte nolineal). Por eso, es natural
considerar la ecuación de Airy (Stokes):
(parte nolineal). Por eso, es natural
considerar la ecuación de Airy (Stokes):
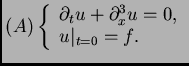
Como 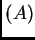 es un problema lineal, a coeficientes constantes, el método de
Fourier se aplica, y se ve que
es un problema lineal, a coeficientes constantes, el método de
Fourier se aplica, y se ve que
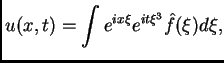
lo que revela la conexión con el problema de Carleson.
Sin embargo, noten que 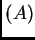 es (lbp),(gbp) en
es (lbp),(gbp) en
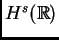 para
todo
para
todo 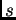 , porque es lineal, a coeficientes constantes, y el
``operador solución"
, porque es lineal, a coeficientes constantes, y el
``operador solución"
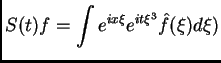
forma un grupo de isometrías en
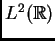 , ya que,
debido al teorema de Plancherel,
, ya que,
debido al teorema de Plancherel,
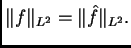
La importancia del problema de Carleson, reside en la desigualdad
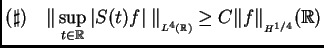
que lo implica. Esta forma fuerte y óptima de ( )
la obtuvimos en un trabajo conjunto con A. Ruiz, en 1983. ¿Cómo
podemos usar
)
la obtuvimos en un trabajo conjunto con A. Ruiz, en 1983. ¿Cómo
podemos usar 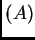 para resolver mKdV?.
La respuesta viene dada por el principio de Duhamel (método de
variación de las constantes en ecuaciones ordinarias). Este dice:
para resolver mKdV?.
La respuesta viene dada por el principio de Duhamel (método de
variación de las constantes en ecuaciones ordinarias). Este dice:
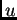 resuelve mKdV si y sólo si
resuelve mKdV si y sólo si
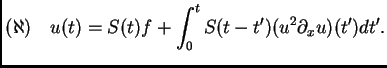
Esta es, por supuesto, una fórmula implícita. Por eso, para
resolver mKdV con
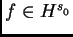 , uno encuentra un espacio de
funciones adecuado, en el cual el lado derecho de
, uno encuentra un espacio de
funciones adecuado, en el cual el lado derecho de 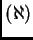 es
una contracción, para
es
una contracción, para
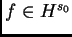 , y por eso tiene un único
punto fijo, que resuelve
, y por eso tiene un único
punto fijo, que resuelve 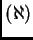 . Esto involucra entender la
interacción entre
. Esto involucra entender la
interacción entre 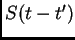 , el operador solución al problema
lineal asociado, y el término no lineal
, el operador solución al problema
lineal asociado, y el término no lineal
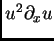 . Es
para entender esta interacción, el operador
. Es
para entender esta interacción, el operador 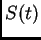 , y la elección
del espacio de funciones, que el análisis armónico desempeña un
papel fundamental, a pesar de que, por ser el problema no lineal,
el método original de Fourier no se aplica. Usando la estimación
, y la elección
del espacio de funciones, que el análisis armónico desempeña un
papel fundamental, a pesar de que, por ser el problema no lineal,
el método original de Fourier no se aplica. Usando la estimación
 , de forma crucial, uno puede probar:
, de forma crucial, uno puede probar:
Teorema 1 [Kenig-Ponce-Vega, 1993]:
mKdV está (lbp) en
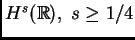 .
.
Este es ``el mismo" 1/4 que en el teorema de Carleson. No
obstante, no había ningún motivo a priori para sospechar que estas
ideas daban un resultado óptimo para el problema no lineal.
Efectivamente, un argumento heurístico de escala, sugiere que no.
Esto es porque, si 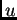 resuelve mKdV, entonces
resuelve mKdV, entonces
también resuelve mKdV, con dato inicial
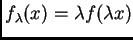 . Observen que
de manera que
Heurísticamente, el ``mejor
. Observen que
de manera que
Heurísticamente, el ``mejor 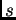 " para (lbp), debe ser el que hace
" para (lbp), debe ser el que hace
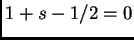 , que es
, que es 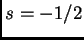 , mucho más chico que
, mucho más chico que 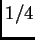 .
Pero, en este problema, la heurística resulta falsa, y el
resultado obtenido por los métodos de análisis armónico es óptimo:
.
Pero, en este problema, la heurística resulta falsa, y el
resultado obtenido por los métodos de análisis armónico es óptimo:
Teorema 2 [Kenig-Ponce-Vega 2000]: mKdV no es
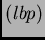 en
en
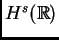 , para
, para 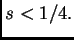
Teorema 3 [Colliander-Keel-Staffilani-Takaoka-Tao,
2001]: mKdV es (gbp) en
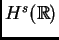 , para
, para
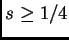 , y no
para
, y no
para 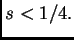
Para dar alguna idea sobre cómo llegamos a la prueba del Teorema
2, recuerden el método de ``inverse scattering" para resolver
mKdV, que reduce la solución del 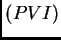 para la ecuación no
lineal, a resolver una familia de problemas espectrales inversos,
lineales. Este método es muy bueno, pero tiene la desventaja de
ser muy rígido, ya que no se aplica a ``pequeñas perturbaciones" y
requiere que los datos iniciales decaigan fuertemente en el
infinito. Más aún, la continuidad de la solución obtenida así, en
espacios funcionales clásicos, es difícil de obtener (sino
imposible). De cualquier manera, el método es muy útil para
ciertos datos. Por ejemplo, para mKdV, el matemático japonés
Wadati (1973) construyó, de esta manera, explícitamente,
soluciones ``breather", que son periódicas en el tiempo, y que
decaen exponencialmente en el espacio. Están dadas por la
siguiente fórmula:
para la ecuación no
lineal, a resolver una familia de problemas espectrales inversos,
lineales. Este método es muy bueno, pero tiene la desventaja de
ser muy rígido, ya que no se aplica a ``pequeñas perturbaciones" y
requiere que los datos iniciales decaigan fuertemente en el
infinito. Más aún, la continuidad de la solución obtenida así, en
espacios funcionales clásicos, es difícil de obtener (sino
imposible). De cualquier manera, el método es muy útil para
ciertos datos. Por ejemplo, para mKdV, el matemático japonés
Wadati (1973) construyó, de esta manera, explícitamente,
soluciones ``breather", que son periódicas en el tiempo, y que
decaen exponencialmente en el espacio. Están dadas por la
siguiente fórmula:
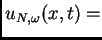
donde
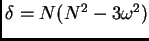 ,
,
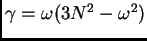 . Cuando
. Cuando
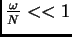 , es fácil ver
que
, es fácil ver
que
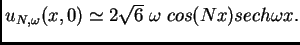
El teorema 2 se prueba usando estas soluciones. ¡El hecho de que
el dato inicial debía ser de esta forma se adivinó usando Análisis
Armónico!
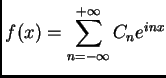
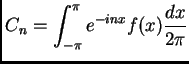
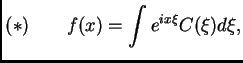
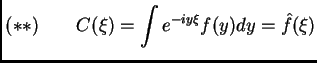
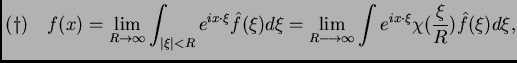
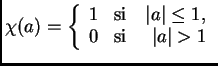
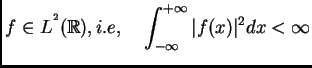
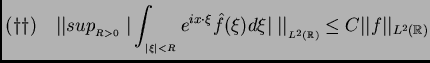
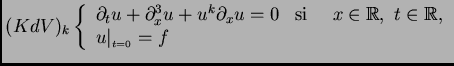
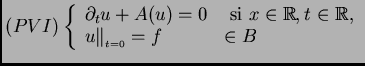
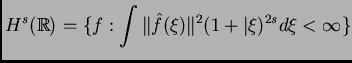
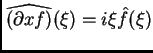 .
Nuestra pregunta entonces es:
¿Para cuáles
.
Nuestra pregunta entonces es:
¿Para cuáles