


Next: A-discriminantes
Up: Discriminantes
Previous: Discriminantes
Primeros ejemplos y motivaciones
Comencemos con un ejemplo bien conocido. Consideremos un polinomio
de grado dos:
y su discriminante
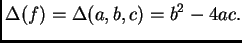 |
(1.1) |
Entonces,
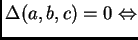 existe
existe
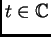 que es raíz doble de
que es raíz doble de 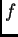
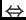 existe
existe
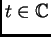 tal que
tal que
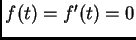
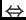 la terna
la terna 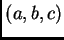 es tal que existe
es tal que existe
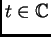 satisfaciendo simultáneamente
satisfaciendo simultáneamente
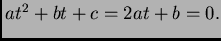 Geométricamente, la hipersuperficie
Geométricamente, la hipersuperficie
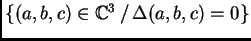 es la
proyección sobre las tres primeras coordenadas
de la subvariedad de
es la
proyección sobre las tres primeras coordenadas
de la subvariedad de
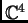 definida por la intersección
de las hipersuperficies
definida por la intersección
de las hipersuperficies
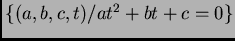 y
y
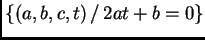 , es decir, se ha eliminado la variable
, es decir, se ha eliminado la variable
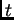 .
En general, dado un polinomio univariado genérico de grado
.
En general, dado un polinomio univariado genérico de grado 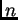 :
es conocida clásicamente la existencia de un polinomio discriminante
:
es conocida clásicamente la existencia de un polinomio discriminante
![$ \Delta(f) = \Delta_n(f) = \Delta (a_0, \dots, a_n) \in \ensuremath{\mathbb{Z}}[a_0, \dots, a_n]$](img17.png) irreducible y único salvo signo que verifica
irreducible y único salvo signo que verifica
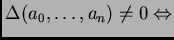 f tiene todas sus raíces simples
f tiene todas sus raíces simples
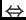
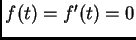 no
tiene solución. Esta noción tiene numerosas aplicaciones en teoría
de números. También podemos asociar un discriminante a
un polinomio univariado ralo (o sparse, en inglés).
Por ejemplo, fijemos los exponentes
no
tiene solución. Esta noción tiene numerosas aplicaciones en teoría
de números. También podemos asociar un discriminante a
un polinomio univariado ralo (o sparse, en inglés).
Por ejemplo, fijemos los exponentes
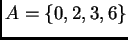 y
y
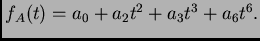 Entonces si
Entonces si 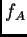 tiene algún cero múltiple, se anula el discriminante
tiene algún cero múltiple, se anula el discriminante
Notar que
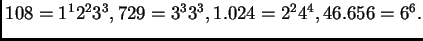 La teoría de discriminantes está íntimamente relacionada a nuestros
esquemas de visión. Lo que vemos de un objeto
La teoría de discriminantes está íntimamente relacionada a nuestros
esquemas de visión. Lo que vemos de un objeto 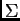 es su borde,
es decir, los puntos
es su borde,
es decir, los puntos 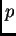 de
de 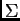 para los cuales el rayo de luz de nuestro
ojo a
para los cuales el rayo de luz de nuestro
ojo a 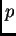 es tangente a
es tangente a 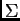 , o más
precisamente, una proyección de su borde. Si suponemos que establecemos
un sistema de coordenadas proyectivas donde nuestros ojos están en el
infinito del eje
, o más
precisamente, una proyección de su borde. Si suponemos que establecemos
un sistema de coordenadas proyectivas donde nuestros ojos están en el
infinito del eje 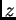 , y la superficie
, y la superficie 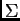 está descripta por
una ecuación polinomial
está descripta por
una ecuación polinomial
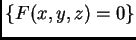 , buscamos la proyección
, buscamos la proyección
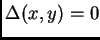 sobre el plano
sobre el plano 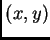 (dada por el discriminante respecto de
(dada por el discriminante respecto de 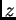 )
de la curva de contacto definida por el par
de ecuaciones
)
de la curva de contacto definida por el par
de ecuaciones
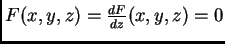 .
Por otro lado, si miramos
.
Por otro lado, si miramos
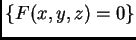 como una familia de curvas planas
como una familia de curvas planas 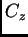 parametrizadas
por
parametrizadas
por 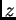 , cuando
, cuando
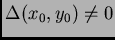 , podemos despejar
, podemos despejar 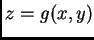 cerca de
cerca de 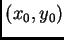 .
Es decir, pasa una única curva
.
Es decir, pasa una única curva 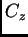 por cada punto. Esto provee unicidad en la
ecuación diferencial implícita
por cada punto. Esto provee unicidad en la
ecuación diferencial implícita
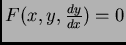 , ya que es localmente
equivalente a la ecuación diferencial explícita de primer orden
, ya que es localmente
equivalente a la ecuación diferencial explícita de primer orden
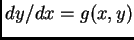 ,
y las soluciones singulares de la ecuación están contenidas en la variedad discriminantal
,
y las soluciones singulares de la ecuación están contenidas en la variedad discriminantal
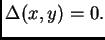 La distancia a la variedad discriminantal está relacionada con la inestabilidad
numérica [#!shub!#]. Consideremos el polinomio de Wilkinson
que claramente tiene
La distancia a la variedad discriminantal está relacionada con la inestabilidad
numérica [#!shub!#]. Consideremos el polinomio de Wilkinson
que claramente tiene  raíces reales. Sin embargo, el polinomio
raíces reales. Sin embargo, el polinomio
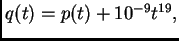 obtenido por una pequeña perturbación
de uno de los coeficientes de
obtenido por una pequeña perturbación
de uno de los coeficientes de 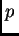 tiene sólo
tiene sólo 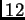 raíces reales
y
raíces reales
y 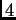 pares de raíces complejas conjugadas, un par con parte
imaginaria aproximadamente
pares de raíces complejas conjugadas, un par con parte
imaginaria aproximadamente
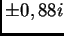 . Podemos explicar este fenómeno
en términos del discriminante. Miremos la familia uniparamétrica
de polinomios
. Podemos explicar este fenómeno
en términos del discriminante. Miremos la familia uniparamétrica
de polinomios
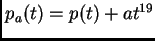 . Entonces
. Entonces
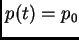 y
y
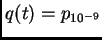 . Para que un par de raíces complejas conjugadas
``se unan'' para dar dos raíces reales, debe haber un valor del parámetro
. Para que un par de raíces complejas conjugadas
``se unan'' para dar dos raíces reales, debe haber un valor del parámetro
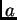 para el cual, ambas raíces coincidan, es decir, es necesario atravesar
los ceros del discriminante
para el cual, ambas raíces coincidan, es decir, es necesario atravesar
los ceros del discriminante
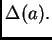 En efecto,
En efecto, 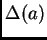 resulta
ser un polinomio de grado
resulta
ser un polinomio de grado 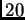 con
con 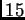 de sus raíces muy cercanas
a 0, y en particular, existe una raíz
de sus raíces muy cercanas
a 0, y en particular, existe una raíz 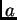 entre 0 y
entre 0 y 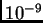 . Es
decir, que los coeficientes de
. Es
decir, que los coeficientes de 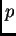 son muy cercanos a los coeficientes
de un polinomio con una raíz múltiple.
son muy cercanos a los coeficientes
de un polinomio con una raíz múltiple.



Next: A-discriminantes
Up: Discriminantes
Previous: Discriminantes


