Ejemplo 1.4
El polinomio univariado genérico de grado 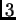
Tomemos
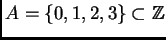 . El polinomio genérico ralo
. El polinomio genérico ralo
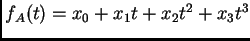 es simplemente el polinomio genérico
de grado
es simplemente el polinomio genérico
de grado 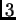 en una variable
y el discriminante es en este caso
en una variable
y el discriminante es en este caso
El polítopo de Newton
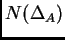
es la cápsula convexa en
del
conjunto
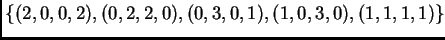
. Notemos
que
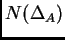
es de hecho un polígono contenido en el plano
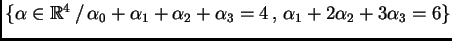
. En particular,
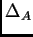
es un
polinomio homogéneo de grado
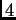
y la dimensión de
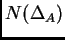
es igual al cardinal de

menos
. Es fácil comprobar que de hecho
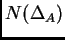
es un cuadrilátero con vértices en los puntos
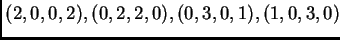
, y el quinto punto resulta ser un
punto interior.
Observemos por otro lado la cápsula convexa de

, es decir el
segmento
![$ I =[0,3]$](img101.png)
en la recta real. Hay cuatro `` triangulaciones''
o particiones posibles de
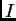
, es decir, cuatro subdivisiones en simples de
dimensión
, o sea segmentos:
Notemos que si en cada caso multiplicamos los valores de
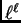
, donde
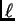
recorre las longitudes de los segmentos en la triangulación, obtenemos
respectivamente
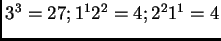
y
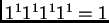
,
que son salvo signo los coeficientes de los monomios en
que
corresponden a los
vértices del polítopo de Newton. Estos vértices
pueden recuperarse a partir de las
triangulaciones de la siguiente manera:
a cada triangulación
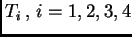
, asignémosle el vector
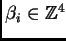
cuya
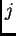
-ésima coordenada,
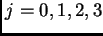
, es igual a la suma de las longitudes de los
segmentos en la triangulación
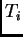
para los cuales el punto
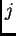
es un extremo.
Entonces los vértices son los puntos
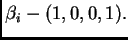
Se llama un dual de Gale de

, a una colección de
vectores enteros
en el plano
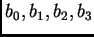
tales que la matriz
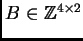
cuyas filas son los vectores
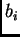
, verifica que sus columnas generan sobre
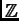
las relaciones enteras de dependencia afín entre los puntos de

.
En nuestro caso, podemos por ejemplo tomar los vectores
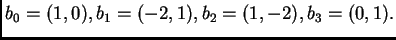
Si dibujamos los
vectores en el plano, las semirrectas por el origen que
generan parten el plano en cuatro conos convexos, que corresponden
precisamente a las
triangulaciones de
.
Ordenemos los vectores
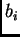
en sentido antihorario, y consideremos
el cuadrilátero
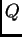
construido a partir del origen yuxtaponiendo estos
vectores, es decir, con vértices en
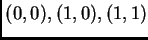
y
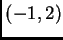
.
Notemos que
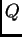
tiene un único punto entero interior, el
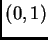
.
Asociemos a cada vector
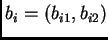
la transformación lineal
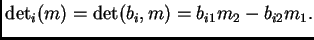
Llamemos
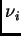
(resp.
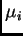
) al mínimo (resp. máximo)
de la funcional
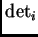
sobre
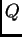
, para
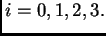
Resulta
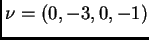
,
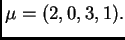
El polítopo de Newton
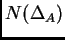
es la imagen de
por la transformación afín que envía el
vector
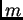
del plano al vector de
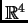
cuya
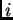
-ésima
coordenada es igual a
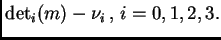
En particular, vértices van a vértices, y es posible
calcular el grado y las homogeneidades del discriminante, como
ya vimos.
Asimismo, es posible recuperar la longitud
de
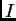
(que es el grado de la variedad tórica
asociada a

) a partir de
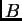
de dos maneras diferentes.
Por un lado, como la semisuma de los máximos
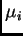
:
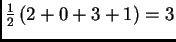
, y por otro, como el producto
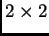
de la suma de las coordenadas positivas en cada una de las
dos columnas de
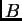
menos un índice asociado a los
vectores
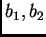
que viven en el interior de cuadrantes
opuestos y que se define como el mínimo de los módulos
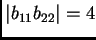
y
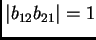
.
Todas las propiedades que hemos enunciado son un caso
particular de teoremas generales.



![]() . El polinomio genérico ralo
. El polinomio genérico ralo
![]() es simplemente el polinomio genérico
de grado
es simplemente el polinomio genérico
de grado ![]() en una variable
y el discriminante es en este caso
en una variable
y el discriminante es en este caso