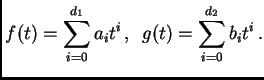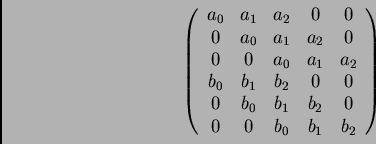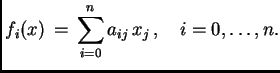Next: Relación entre discriminantes y
Up: Resultantes
Previous: Resultantes
Comencemos con dos ejemplos clásicos.
Ejemplo 2.1
Polinomios en una variable
Fijemos dos enteros positivos 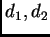 y consideremos
polinomios genéricos en una variable con estos grados:
y consideremos
polinomios genéricos en una variable con estos grados:
El sistema
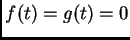
es en general sobredeterminado
y no tiene solución.
Es clásicamente conocido que existe un polinomio irreducible
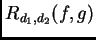
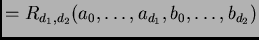
con coeficientes enteros e irreducible llamado
la
resultante de
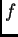
y
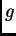
, cuya anulación en los
coeficientes de
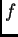
y
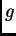
es equivalente al hecho de que
los dos polinomios tengan alguna raíz compleja en común.
Geométricamente, la hipersuperficie
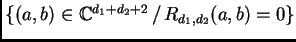
es la
proyección de la variedad de incidencia
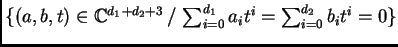
;
o sea, se ha eliminado la variable
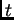
.
Un conocido teorema de Sylvester permite calcular
la resultante como el determinante de una matriz
de tamaño
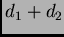
cada una de cuyas entradas
es un coeficiente de alguno de los polinomios, o cero.
Por ejemplo, si
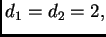
la resultante es el
siguiente polinomio en
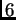
variables
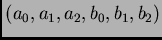
:
y se calcula como el determinante de la siguiente matriz
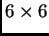
:
Ejemplo 2.2
El caso homogéneo
Consideremos
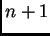
formas genéricas de grado
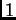
en
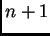
variables:
Entonces, existe
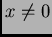
tal que es solución del sistema
lineal homogéneo
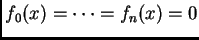
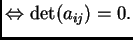
Es decir, que el determinante es un polinomio en los coeficientes
de las formas dadas que permite resolver el problema de eliminación
de decidir si existe o no una solución no trivial del sistema.
En general, fijados grados

, consideremos
polinomios homogéneos genéricos con estos grados
Cayley, Sylvester, Bézout y Macaulay demostraron la
existencia de un polinomio irreducible
![$ {\rm Res}_{d_0,\dots, d_n}
\in \ensuremath{\mathbb{Z}}[ a^i_\alpha\, , \, i=0,\dots,n, \vert\alpha\vert = d_i]$](img164.png)
que se anula
en los coeficientes de
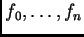
si y sólo si existe
una raíz común
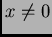
no trivial del sistema
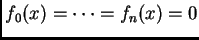
, es decir, si y sólo si existe
una raíz común en el espacio proyectivo compacto
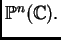
Cuando todos los grados son iguales a
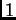
,
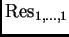
coincide con el determinante del sistema lineal.
Así como el determinante de un sistema lineal puede utilizarse
no sólo para verificar la existencia de soluciones no triviales de
un sistema homogéneo, sino que puede utilizarse también para
calcular la solución de un sistema no homogéneo, es posible
utilizar las resultantes para ``resolver'' sistemas algebraicos no lineales.
Dados
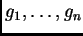 polinomios de grados respectivos
polinomios de grados respectivos
 ,
denotemos por
,
denotemos por
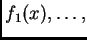
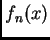 sus respectivas
homogeneizaciones
sus respectivas
homogeneizaciones
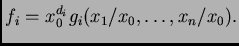 El polinomio univariado
El polinomio univariado
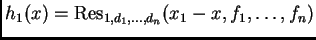 se anula en todos aquellos puntos
se anula en todos aquellos puntos
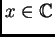 que
sean la primer coordenada de una raíz común en
de los polinomios
que
sean la primer coordenada de una raíz común en
de los polinomios
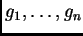 . Es decir,
usando resultantes es posible eliminar
. Es decir,
usando resultantes es posible eliminar 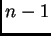 variables, y reducir la búsqueda
de las raíces comunes de un sistema multivariado
a la búsqueda de raíces de polinomios en una variable.
Por supuesto, esto es útil únicamente si podemos asegurar que el polinomio
obtenido no es idénticamente cero. Una condición necesaria
es que los polinomios
variables, y reducir la búsqueda
de las raíces comunes de un sistema multivariado
a la búsqueda de raíces de polinomios en una variable.
Por supuesto, esto es útil únicamente si podemos asegurar que el polinomio
obtenido no es idénticamente cero. Una condición necesaria
es que los polinomios
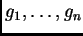 tengan finitas raíces comunes.
Observemos el siguiente ejemplo:
tengan finitas raíces comunes.
Observemos el siguiente ejemplo:
Ejemplo 2.3
Polinomios con ``soporte cuadrado''
Consideremos los siguientes polinomios genéricos ralos con
soporte en el cuadrado unitario:
Para coeficientes genéricos, estos
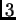
polinomios en
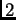
variables
de grado
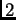
no tienen raíces comunes en
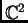
. Sin embargo,
sus homogeneizados se anulan en los puntos
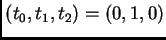
y
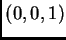
, para toda elección de coeficientes. Por lo
tanto
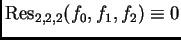
, y no provee
ninguna información.
Es necesario entonces considerar resultantes ``a medida'', de
acuerdo al soporte de los polinomios. Esto ha conducido a la noción
de  -resultantes, o más generalmente, de
-resultantes, o más generalmente, de
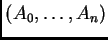 -resultantes,
donde
-resultantes,
donde
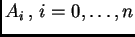 , son subconjuntos finitos de puntos
enteros en
, son subconjuntos finitos de puntos
enteros en
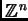 [10,14,15]. La familia de soportes
[10,14,15]. La familia de soportes
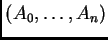 se dice esencial cuando para todo subconjunto propio
se dice esencial cuando para todo subconjunto propio
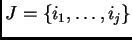 de
de
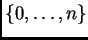 , la menor variedad afín que contiene a los
puntos de la suma de Minkowski
, la menor variedad afín que contiene a los
puntos de la suma de Minkowski
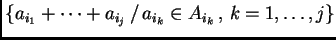 es de dimensión
mayor o igual que
es de dimensión
mayor o igual que 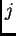 . Si esta propiedad se verifica, entonces
existe un polinomio irreducible con coeficientes enteros
. Si esta propiedad se verifica, entonces
existe un polinomio irreducible con coeficientes enteros
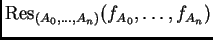 definido
salvo signo, que se anula cuando existe un punto
definido
salvo signo, que se anula cuando existe un punto
 que es una raíz común de los polinomios ralos
que es una raíz común de los polinomios ralos
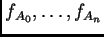 con soporte en
con soporte en
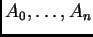 respectivamente. De hecho, la resultante se anula si y sólo
si las clausuras de las hipersuperficies
respectivamente. De hecho, la resultante se anula si y sólo
si las clausuras de las hipersuperficies
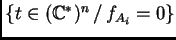 (
(
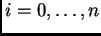 )
tienen intersección vacía en una apropiada
compactificación tórica de
)
tienen intersección vacía en una apropiada
compactificación tórica de
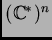 asociada a la familia de soportes.
En la última década, el uso de resultantes como una herramienta
computacional para la resolución de sistemas de ecuaciones polinomiales,
ha renovado ampliamente el interés en su estudio y en la búsqueda de
fórmulas explícitas para su cálculo [6,7].
asociada a la familia de soportes.
En la última década, el uso de resultantes como una herramienta
computacional para la resolución de sistemas de ecuaciones polinomiales,
ha renovado ampliamente el interés en su estudio y en la búsqueda de
fórmulas explícitas para su cálculo [6,7].



Next: Relación entre discriminantes y
Up: Resultantes
Previous: Resultantes
![]() y consideremos
polinomios genéricos en una variable con estos grados:
y consideremos
polinomios genéricos en una variable con estos grados:
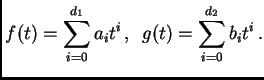
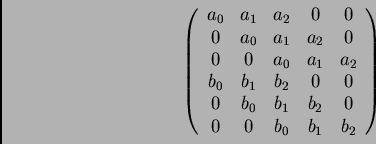



![]() y consideremos
polinomios genéricos en una variable con estos grados:
y consideremos
polinomios genéricos en una variable con estos grados: