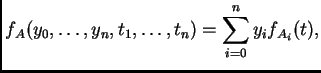Relación entre discriminantes y resultantes

Veremos cómo es posible obtener discriminantes a partir de resultantes, y recíprocamente. Comencemos por un ejemplo.

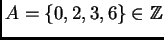
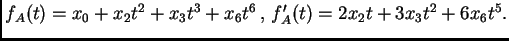
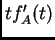
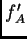
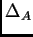
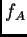
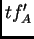
Ejemplo 2.4   Fijemos $A = \{0,2,3,6\} \in \ensuremath{\mathbb{Z}}$, $f_A (t) = x_0 + x_2 t^2 + x_3 t^3 + x_6 t^6\, , \, f'_A(t) = 2 x_2 t + 3 x_3 t^2 + 6 x_6 t^5.$ Notemos que el polinomio $t f'_A(t)$ tiene soporte contenido nuevamente en $A$, y las mismas raíces que $f'_A$ en $\ensuremath{\mathbb{C}}^*$. 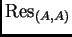Como el $A$-discriminante $\Delta_A$ se anula cuando los polinomios $f_A$ y $t f'_A$ tienen una raíz común no nula, y la resultante ${\rm Res}_{(A,A)}$ se anula en un par de polinomios cuando tienen una raíz común no nula, parecería que ambos polinomios coinciden. Sin embargo,

$${\rm Res}_{(A,A)}(f_A, t f'_A(t)) \, = \, x_0 \, x_6^2 \, \Delta_A(x).$$

Es decir, que el discriminante es factor de la resultante, pero han aparecido otros.

En general, fijado un conjunto finito $A \subset \ensuremath{\mathbb{Z}}^n$, llamemos discriminante total al polinomio $E_A \, = \, {\rm Res}_{(A,\dots,A)} (f_A, t_1 \frac {\partial f_A} {\partial t_1}, \dots, t_n \frac {\partial f_A} {\partial t_n}).$ Entonces, tenemos la factorización

$$E_A \, = \, \prod_{A' \subseteq A\, , \, A' \, {\rm facial }} \Delta_{A'}^{\delta_{A'}},$$ (2.1)

donde $A'$ es un subconjunto facial de $A$ si se obtiene como la intersección de $A$ con una de las caras de su cápsula convexa, y los exponentes $\delta_{A'}$ son enteros positivos. Estos exponentes en general no son explícitos pero siempre $\delta_A =1.$

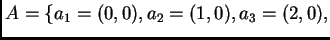
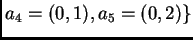
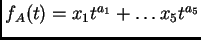
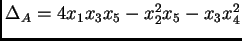
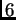
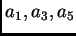
Ejemplo 2.5   Consideremos $A = \{ a_1 = (0,0) , a_2 = (1,0), a_3 = (2,0),$ $a_4 = (0,1), a_5 = (0,2) \}$, y notemos como antes $f_A (t) = x_1 t^{a_1} + \dots x_5 t^{a_5}$ el polinomio bivariado genérico con exponentes en $A$. Entonces, el discriminante $\Delta_A = 4 x_1 x_3 x_5 - x_2^2 x_5 - x_3 x_4^2$ y $A$ tiene $6$ subconjuntos faciales propios, los tres vértices $a_1, a_3, a_5$ y los tres lados del triángulo que es la cápsula convexa de $A$. 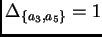Entonces, $\Delta_{\{a_3, a_5\}} = 1$ y el discriminante total se factoriza como

$$E_A (x) \, = \, x_1 \, x_3 \, x_5 \, (x_1 x_3 - 4 x_2^2) \, (x_1 x_5 - 4 x_4^2) \, \Delta_A(x).$$

Veamos ahora como presentar la resultante de una familia esencial como un discriminante, mediante lo que se conoce con el nombre de Cayley trick, ya que Cayley fue el primero en proponerlo. Dados $A_0, \dots, A_n \subset \ensuremath{\mathbb{Z}}^n$, definamos la configuración de Cayley asociada $A \subset \ensuremath{\mathbb{Z}}^{2n+1}$ como

$$A \, = \, e_0 \times A_0 \cup \dots \cup e_n \times A_n,$$

donde $e_i$ es el $i$-ésimo vector de la base canónica en $Z^{n+1}$.

Ejemplo 2.6   Supongamos que $n=1$, $A_0= \{0,1,2\}$ y $A_1 = \{0,1\}$. Entonces $e_0 = (1,0), e_1 = (0,1)$ y la configuración de Cayley asociada $A \, = \, \{(1,0,0), (1,0,1), (1,0,2), (0,1,0), (0,1,1)\}$ consta de $5$ puntos cuya cápsula convexa es un trapecio en el plano $\{ v \in \ensuremath{\mathbb{R}}^3 \, / \, v_1 + v_2 = 1 \}$.

Claramente, las configuraciones de Cayley son muy especiales. Notemos que el polinomio genérico ralo con exponentes en $A$ se escribe como

$$f_A(y_0, \dots, y_n, t_1,\dots, t_n) = \sum_{i=0}^n y_i f_{A_i}(t),$$

donde $f_{A_i}$ es el polinomio genérico ralo con exponentes en $A_i$ para $i=0,\dots,n.$ Luego, la derivada parcial de $f_A$ con respecto a la variable $y_i$ es precisamente $f_{A_i}$. Si $A_0, \dots, A_n$ es esencial, resulta que

$${\rm Res}_{(A_0, \dots, A_n)} = \Delta_A.$$

Sin embargo, hay una propiedad importante que permite distinguir entre discriminantes y resultantes. Con este fin, introduzcamos los sistemas $A$-hipergeométricos.