U M A - Unión Matemática Argentina

Bases de "wavelets" en espacios de tipo homogéneo

Hugo Aimar

dedicado a Carlos Segovia Fernández

Hugo Aimar: IMAL-CONICET y Departamento de Matemática, FIQ Universidad Nacional del Litoral. (3000) Santa Fe, Argentina

Un espacio de tipo homogéneo, hablando generalmente, es un espacio métrico de dimensión finita.

(1) Por el teorema de metrización de espacios casi-métricos de Macías-Segovia, toda casi-métrica equivale a una potencia de una métrica o, más generalmente, a una función de una métrica:

$d(x,y)\leq K(d(x,z)+d(z,y)); d\sim \rho^{\beta}$
$d(x,y)\leq \eta(d(x,z)+d(z,y)); d\sim \psi({\rho})$

(2) Dispersión: $A\subset X, \varepsilon>0$ . es $\varepsilon$ -disperso si $d(x,y)\geq\varepsilon,\; x\in A \; y\in A, \; x\neq y.$ Dimensión Finita: $\exists N>0/\forall x\in X \forall r>0$ , para todo $A \; \frac{r}{2}$ -disperso,

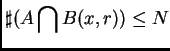
$\displaystyle \sharp (A\bigcap B(x,r))\leq N$

Todo subconjunto del espacio $\hbox{\rm I\hskip-2pt R}^{n}$ , con la restricción de las métricas usuales resulta un e.t.h.
Con esta noción débil de Homogeneidad se tiene - separabilidad; - base numerable para la topología; - coincidencia de acotación y acotación total; - con completitud, Heine-Borel; - lemas de cubrimiento de Wiener, Whitney, Vitali (no Besicovich)
Si es un e.m. de dimensión finita en el sentido descripto, entonces tiene dimensión de Hausdorff finita.
Si es un e.m. completo de dimensión finita, entonces existe una medida de Borel $\mu$ que satisface la propiedad de duplicación (doblante o doubling)

$\displaystyle 0<\mu(B(x,2r))\leq A\mu(B(x,r))<\infty.$

Si en el e.m. hay una medida de Borel $\mu$ que satisface una propiedad de duplicación, entonces tiene dimensión finita.

Estos resultados fueron obtenidos por varios autores con diferentes hipótesis (Coiffman, de Guzmán, Weiss, Volerg, Konyagin, Wu, Luukainnen,...).

Problemas analíticos en espacios generales.

Multiplicadores: el Análisis de Fourier transforma operadores de convolución en operadores de multiplicación (diagonaliza).
Acotación en $L^{2}$ de la integral de Cauchy sobre curvas Lipschitz. Coifman-Jones-Semmes: construyeron una base de $L^{2}$ sobre la curva en la que el operador de Cauchy es casi -diagonal.
Cuando ponemos una métrica o una casi-métrica en un conjunto para modelar un operador particular, generalmente obtenemos núcleos controlados por esa distancia.
Un objetivo es construir bases de los espacios funcionales clásicos para las cuales estos operadores sean casi-diagonales.
En $\hbox{\rm I\hskip-2pt R}$ , $\hbox{\rm I\hskip-2pt R}^{n}$ , la construcción de wavelets de estructura compleja depende del Análisis de Fourier clásico.
La base de Haar se puede construir en $\hbox{\rm I\hskip-2pt R}^{1}$ prescindiendo de la Transformada de Fourier.
Regularización de bases ortonormales producen bases de Riesz.
Regularizar en e.t.h. es posible por procedimientos similares a la convolución.

Bases de Haar en e.t.h.

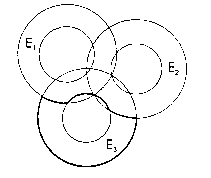
Teselados diádicos. Sea $\{x_{\alpha}: \; \alpha \in \hbox{\rm I\hskip-2pt N}\}$ una sucesión 1-dispersa maximal en . La maximalidad asegura que la familia de bolas $\{B(x_{\alpha}, 1): \, \alpha \in \hbox{\rm I\hskip-2pt N}\}$ constituye un cubrimiento de . La ``uno dispersión'' asegura que las bolas $\{B(x_{\alpha},\frac{1}{2k})\}$ son disjuntas dos a dos. Esto permite un proceso de disjunción de las bolas $B(x_{\alpha}, 1)$ que preserve las bolas $B(x_{\alpha},\frac{1}{2k})$ .

Bases de Haar en e.t.h

Cada $(E_{\alpha}, d)$ , $\alpha \in \hbox{\rm I\hskip-2pt N}$ es también un e.t.h. Podemos entonces repetir el procedimiento tomando en $(E_{\alpha}, d)$ un conjunto maximal que sea $\frac{1}{2}$ -disperso. Para por ejemplo

Bases de Haar en e.t.h

Más formalmente

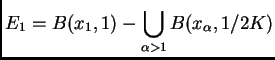
$\displaystyle E_{1}=B(x_{1},1)-\bigcup_{\alpha>1}B(x_{\alpha},1/2K)$

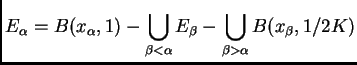
$\displaystyle E_{\alpha}=B(x_{\alpha},1)-\bigcup_{\beta<\alpha}E_{\beta}-\bigcup_{\beta>\alpha}B(x_{\beta},1/2K)$

Una sucesión de árboles (bosque) es un buen procedimiento para ``contabilizar" la historia de una región del espacio al iterar:

$A=\bigcup_{n=1}^{\infty}A_{n}; \; A_{n}\subset \hbox{\rm I\hskip-2pt N}^{n}$ ; - $\alpha\in A_{n}, \; l(\alpha)=n$ (generación n-ésima); - $\alpha\in A_{n}, \; n\geq 2, \; \alpha=(\beta,\gamma), \; \beta\in \hbox{\rm I\hskip-2pt N}^{n-1}, \; \gamma\in \hbox{\rm I\hskip-2pt N},$ entonces $\beta\in A_{n-1}$ y $\gamma\leq C(K,N)$ ; - Para toda $\beta\in A_{n-1}(n\geq 2) \; \{\gamma\in \hbox{\rm I\hskip-2pt N}:\alpha=(\beta,\gamma)\in A_{n}\}$ es un intervalo en $\hbox{\rm I\hskip-2pt N}$ que contiene al menos a 1; - $A_{1}$ es finito si y sólo si es acotado.

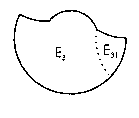
De este modo encontramos que existen: $\mathcal{D}=\{E_{\alpha}:\alpha\in A\}$ una familia de borelianos y una sucesión $\{x_{\alpha}: \alpha\in A\}\subset X$ tales que

- $\alpha=(\alpha',\alpha_{k+1},\ldots,\alpha_{n})\in A, \; l(\alpha')=k, \quad k<n \Rightarrow \alpha'\in A$ y $E_{\alpha}\subseteq E_{\alpha'}$ ;

- $x_{\alpha}\in E_{\alpha},\; \forall \alpha\in A;$

- $E_{\alpha}\subset B(x_{\alpha}, (2K)^{1-l(\alpha)})$ ;

- $X=\bigcup_{l(\alpha)=m}E_{\alpha}, \quad \forall m\in \hbox{\rm I\hskip-2pt N}$ ;

- $E_{\alpha}\cap E_{\beta}=\emptyset, \quad \alpha\in A , \; \beta \in A \;\; \alpha \neq \beta,\; l(\alpha)=l(\beta);$

- $\alpha\in A \wedge \beta \in A \Longrightarrow E_{\alpha}=E_{\beta},\; E_{\alpha}\cap E_{\beta}=\emptyset ,\; E_{\alpha}\subset E_{\beta}$ o $E_{\beta}\cap E_{\alpha}$

- $\{x_{\alpha}: \alpha\in A\}$ es denso en .

Ahora ``ponemos" en una medida $\mu$ (que duplique o no) finita y positiva sobre bolas. Tenemos los siguientes resultados analíticos básicos.

Maximal de H-L asociado a $\mathcal{D}$ . Tipo débil uno-uno y acotado en $L^{p}$ .
Si $\mu$ es regular, por el Teor. de M-S, existe un $\alpha>0$ tal que las funciones con soporte compacto y de clase Lipschitz $\alpha$ es denso en $L^{p} (p<\infty)$ .
$\mathcal{D}$ es una base de diferenciación.
AMR (Análisis Multiresolución), ,

$\displaystyle V_{n}=\{f\in L^{2}:f \mathrm{constante\ sobre\ } E_{\alpha} \mathrm{con\ } l(\alpha)=n+1\}$

$L^{2}=\overline{\bigcup_{n=0}^{\infty}V_{n}}$ .

Construcción de una BON de $L^{2}$ . Sea $\mathcal{X}_{\alpha}=\mathcal{X}_{E_{\alpha}} \quad ; \quad E_{\alpha}\in \mathcal{D}$ .

$\{\frac{\mathcal{X}_{\alpha}}{\sqrt{\mu(E_{\alpha})}}=h_{\alpha}; l(\alpha)=1\} \mathrm{BON} V_{0}$
Fijamos $\alpha_{1}\quad (\alpha_{1}=3 \mathrm{en\ el\ dibujo})$
$\{\mathcal{X}_{3}, \mathcal{X}_{32}, \mathcal{X}_{33}, \ldots, \mathcal{X}_{36}\}$ es una base del espacio de las funciones sobre $E_{3}$ que son constantes en cada $E_{3i},\quad i=1, 2, \ldots, 6$ .
Ortonormalización ``guardando" $\frac{\mathcal{X}_{3}}{\sqrt{\mu(E_{3})}}$ .

Obtenemos funciones $h_{32}, h_{33}, \ldots, h_{36}$ tales que

$\displaystyle \{h_{3}, h_{32}, h_{33}, \ldots, h_{36}\}$

es BON de ese espacio. Este procedimiento es general y podemos escribir

$\displaystyle V_{1}=V_{0}\oplus W_{1}$

con $W_{1}$ generado por $\{h_{\alpha}:l(\alpha)=2;\alpha_{2}\neq 1\}$ . Entonces

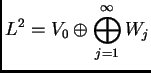
$\displaystyle L^{2}=V_{0}\oplus \bigoplus_{j=1}^{\infty}W_{j}$

Existe $\{h_{\beta}:\beta\in B\}$ BON de $L^{2}$ que es una base incondicional de $L^{p}(1<p<\infty)$ . Soporte de $h_{\beta}\subset B(\mathcal{X}_{\beta},(\frac{1}{2K})^{l(\beta)-2})$ . Y tenemos la relación fundamental para la norma de en téminos de los coeficientes de Haar.

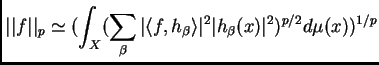
$\displaystyle \vert\vert f\vert\vert _{p}\simeq (\int_{X}(\sum_{\beta}\vert\langle f,h_{\beta}\rangle\vert^{2}\vert h_{\beta}(x)\vert^{2})^{p/2}d\mu(x))^{1/p}$

Que se obtiene de dos teorías de integrales singulares:

Burkholder (Martingalas).
Calderón-Zygmund

dependiendo del grado de degeneración de la familia diádica $\mathcal{D}$ medida en términos del cociente $\frac{\mu(E_{\alpha})}{\mu(E_{\alpha})}$ donde $E_{\beta}$ es hijo de $E_{\alpha}$ . La ventaja de la primera es que no necesita propiedad de duplicación. Los procesos de regularización en e.t.h. permiten construir bases de Riesz regulares que, aunque no satisfacen las condiciones de ortogonalidad, son adecuadas para el análisis de operadores. Carlos Kenig me hizo notar que una descomposición diádica similar a la expuesta aquí ha sido construida por M. Christ para producir una prueba del Teorema T(1) en el contexto de martingalas.