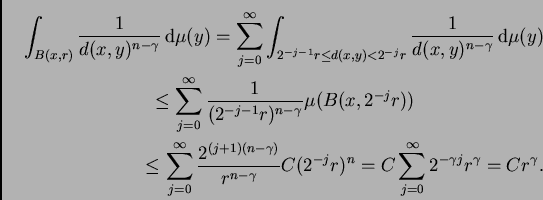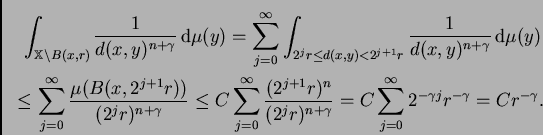Next: Integrales fraccionarias. Teorema de
Up: Operadores fraccionarios para medidas
Previous: Introducción
Mientras no se diga otra cosa, en todo lo que sigue,
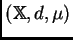 va a ser un espacio `` no homogéneo''. Esto
significa que
va a ser un espacio `` no homogéneo''. Esto
significa que 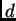 es una distancia en
es una distancia en
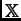 y
y 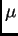 una medida de
Borel en
una medida de
Borel en
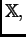 tales que, para cada bola
se
cumple
tales que, para cada bola
se
cumple
|
(2.1) |
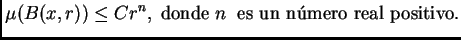 |
A veces nos referiremos a la condición (
2.1) diciendo que la
medida 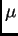 es
es 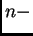 dimensional.
Aunque en un espacio métrico arbitrario, una bola no determina de
forma unívoca ni su centro ni su radio, cuando hablemos de ``
la bola
dimensional.
Aunque en un espacio métrico arbitrario, una bola no determina de
forma unívoca ni su centro ni su radio, cuando hablemos de ``
la bola 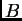 '', daremos por sobreentendido, que hemos elegido
para ella un centro y un radio. Así tiene sentido decir que si
'', daremos por sobreentendido, que hemos elegido
para ella un centro y un radio. Así tiene sentido decir que si 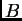 es una bola y
es una bola y 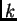 es un número real positivo, denotaremos por
es un número real positivo, denotaremos por 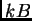 la bola con el mismo centro que
la bola con el mismo centro que 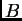 y radio
y radio 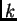 veces el de
veces el de
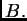
Demostración. Si
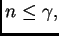 (
2.2) se sigue inmediatamente de
(2.1). Si
(
2.2) se sigue inmediatamente de
(2.1). Si 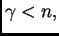 escribimos
escribimos
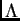
Demostración.



Next: Integrales fraccionarias. Teorema de
Up: Operadores fraccionarios para medidas
Previous: Introducción