Bibliography

C

M. Christ. Singular Integral Operators. Regional Conf. Ser. in Math. 77, Amer. Math. Soc., Providence, 1990.

CG

R. Coifman and M. de Guzmán. Singular integrals and multipliers on homogeneous spaces. Collection of articles dedicated to Alberto González Domínguez on his sixty-fifth birthday. Rev. Un. Mat. Argentina 25 (1970/71), 137-143.

CM

R. Coifman and Y. Meyer. Wavelets. Calderón-Zygmund and multilinear operators Cambridge studies in advanced Mathematics 48, 1997.

CW1

R. Coifman and Guido Weiss. Analyse harmonique non-commutative sur certains espaces homogènes. Étude de certaines intégrales singulières. Lecture Notes in Mathematics, Vol. 242. Springer-Verlag, Berlin-New York, 1971. v+160 pp.

CW2

R. Coifman and Guido Weiss. Extensions of Hardy spaces and their use in analysis. Bull. Amer. Math. Soc. 83 (1977), no. 4, 569-645.

D1

Guy David. Opérateurs intégraux singuliers sur certaines courbes du plan complexe. Ann. Sci. École Norm. Sup. (4) 17 (1984), no. 1, 157-189.

D2

Guy David. Wavelets and Singular Integrals on Curves and Surfaces. Lecture Notes in Math. 1465, Springer-Verlag, Berlin, 1991.

GM1

J. García-Cuerva and J.M. Martell. Weighted inequalities and vector-valued Calderón-Zygmund operators on non-homogeneous spaces. Public. Math. Vol 44(2), (2000), pp. 613-640.

GM2

J. García-Cuerva and J.M. Martell. Two-weight norm inequalities for maximal operators and fractional integrals on non-homogeneous spaces. Indiana University Mathematics Journal, Vol 50(3), (2001)

GGW

A. E. Gatto, C. E. Gutiérrez, R. L.Wheeden. On weighted fractional integrals. Conference on harmonic analysis in honor of Antoni Zygmund, Vol. I, II (Chicago, Ill., 1981), 124-137, Wadsworth Math. Ser., Wadsworth, Belmont, Calif., 1983.

GSV

A. E. Gatto, C. Segovia, S. Vági, On fractional differentiation and integration on spaces of homogeneous type, Rev. Mat. Iberoamericana 12, no. 1,(1996) 111-145.

GV1

A. E. Gatto, S. Vági, Fractional integrals on spaces of homogeneous type. Analysis and partial differential equations, 171-216, Lecture Notes in Pure and Appl. Math., 122, Dekker, New York, 1990.

GV2

A. E. Gatto, S. Vági, On functions arising as potentials on spaces of homogeneous type. Proc. Amer. Math. Soc. 125, no. 4,(1997) 1149-1152.

MMNO

J. Mateu, P. Mattila, A. Nicolau and J. Orobitg. 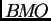for non doubling measures. Duke Math. J. 102 (2000), no. 3, 533-565.

NTV1

F. Nazarov, S. Treil and A. Volberg. Cauchy integral and Calderón-Zygmund operators on nonhomogeneous spaces. Int. Math. Res. Not. 15 (1997), 703-726.

NTV2

F. Nazarov, S. Treil and A. Volberg. Weak type estimates and Cotlar inequalities for Calderón-Zygmund operators in nonhomogeneous spaces. Int. Math. Res. Not. 9 (1998), 463-487.

NTV3

F. Nazarov, S. Treil and A. Volberg. Tb-theorem on non-homogeneous spaces, preprint 1999.

S

E. M. Stein Singular integrals and differentiability properties of functions. Princeton Univ. Press. Princeton, N.J., 1970.

To1

X. Tolsa. 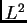-boundedness of the Cauchy integral operator for continuous measures. Duke Math. J. 98:2 (1999), 269-304.

To2

X. Tolsa. Cotlar's inequality and existence of principal values for the Cauchy integral without the doubling condition. J. Reine Angew. Math. 502 (1998), 199-235.

To3

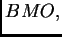
X. Tolsa, 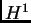and Calderón-Zygmund operators for non-doubling measures, Math. Ann. To appear

Z

A. Zygmund, Trigonometric series, second edition, Cambridge University Press, Cambridge, London, New York, 1968.