


Next: Bibliography
Up: Operadores fraccionarios para medidas
Previous: El espacio `` regular''
Los espacios de Lipschitz que hemos considerado hasta ahora, sólo
dependen de la métrica, y no de la medida. Es un hecho notable que
basten dichos espacios para contener las imágenes por los
operadores fraccionarios de las funciones de 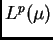 para
para
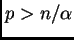 (Teorema
5.2). En particular el Teorema
5.2 implica que si
(Teorema
5.2). En particular el Teorema
5.2 implica que si
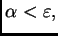 entonces
entonces
 es acotado de
es acotado de
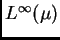 en
en
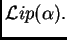 Tiene sentido preguntarse por la imagen
del espacio mayor
Tiene sentido preguntarse por la imagen
del espacio mayor
 Esta pregunta nos lleva a introducir
los espacios de Lipschitz `` grandes''.
El contexto es aquí, de nuevo,
Esta pregunta nos lleva a introducir
los espacios de Lipschitz `` grandes''.
El contexto es aquí, de nuevo,
 con una medida
con una medida 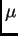
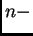 dimensional.
dimensional.
Definición 7.1
Para
![$ \alpha\in ]0,1[,$](img289.png)
llamaremos
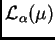
al
espacio de las clases de equivalencia módulo constantes de
funciones localmente integrables con respecto a
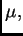
que
satisfacen la condición siguiente:
Para cada par de bolas
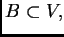
si llamamos
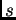
al radio de

se tiene, con una constante fija
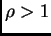
|
(7.1) |
|
|
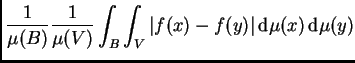 |
|
|
|
|
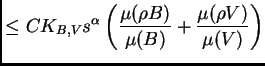 |
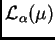 es un espacio de Banach con la norma
dada por la menor constante
es un espacio de Banach con la norma
dada por la menor constante  que hace cierta la desigualdad de
más arriba.
Nótese que la condición de la última definición equivale a pedir
juntas las dos propiedades siguientes:
que hace cierta la desigualdad de
más arriba.
Nótese que la condición de la última definición equivale a pedir
juntas las dos propiedades siguientes:
|
(7.2) |
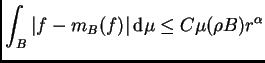 |
para toda bola  de radio
de radio 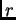 y
y
|
(7.3) |
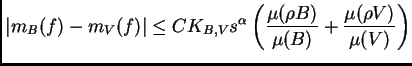 |
para todo par de bolas
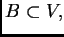 llamando
llamando 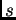 al radio de
al radio de
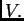 En estas dos condiciones
En estas dos condiciones 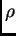 es una constante fija tal que
es una constante fija tal que
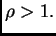 Se demuestra, tal como hace Tolsa para
Se demuestra, tal como hace Tolsa para
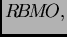 que el espacio
obtenido no depende de
que el espacio
obtenido no depende de 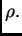
Teorema 7.2
Sea
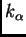
un núcleo fraccionario con regularidad
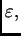
y
sea
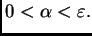
Entonces

es un
operador acotado de
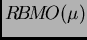
en
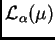
si y sólo si
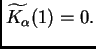
Demostración. La necesidad y el hecho de que
son exactamente como en la demostración del teorema
5.3. De hecho, en cierto sentido el teorema que vamos a
demostrar ahora es la versión 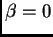 del teorema
5.3 .
Para probar la suficiencia, suponemos
del teorema
5.3 .
Para probar la suficiencia, suponemos
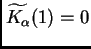 y tomamos
y tomamos
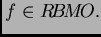 Sabemos que
para
Sabemos que
para 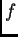 existe una colección de números
existe una colección de números
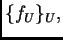 donde
donde 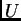 son las bolas centradas en puntos del soporte de la medida, tales
que
y, además
para cada par de bolas
son las bolas centradas en puntos del soporte de la medida, tales
que
y, además
para cada par de bolas
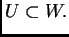 Esta es la caracterización de
Esta es la caracterización de
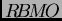 con la que Tolsa obtiene la desigualdad de John-Nirenberg.
Sean dos bolas
con la que Tolsa obtiene la desigualdad de John-Nirenberg.
Sean dos bolas
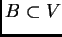 de radios respectivos
de radios respectivos 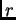 y
y 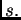 Escribimos, para
Escribimos, para 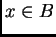 e
e 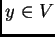
Nuestro propósito es demostrar (
7.1). A partir de
(7.4) obtenemos
Ahora estudiamos la aportación de cada uno de los
cuatro términos del segundo miembro a la media doble.
Para el primer término tenemos, eligiendo un
![$ p\in]1,n/\alpha[$](img209.png) y
el correspondiente
y
el correspondiente 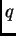 tal que
tal que
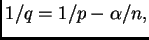 de forma que
podamos aplicar el teorema de Hardy-Littlewood-Sobolev
de forma que
podamos aplicar el teorema de Hardy-Littlewood-Sobolev
donde hemos usado la desigualdad de John-Niremberg probada por
Tolsa para
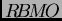 y el hecho de que
y el hecho de que
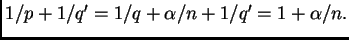 Hemos obtenido
que sirve para nuestros propósitos.
El tratamiento del tercer término es muy parecido. Lo vemos a
continuación.
Hemos obtenido
que sirve para nuestros propósitos.
El tratamiento del tercer término es muy parecido. Lo vemos a
continuación.
Esto nos da
también en línea con lo que buscamos.
El segundo término es un tanto especial. Veamos cómo podemos
acotarlo.
Esta estimación no es exactamente la que queremos, debido a la
presencia del exponente
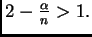 Posponemos, por el
momento la discusión de cómo solucionar este inconveniente y
pasamos a estudiar el cuarto término.
Posponemos, por el
momento la discusión de cómo solucionar este inconveniente y
pasamos a estudiar el cuarto término.
donde hemos usado el lema 2 para obtener el segundo sumando. Dicho
sumando está dominado por
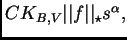 que
es lo que queremos. Sólo tenemos que ocuparnos del primer sumando.
Lo acotamos por
que
es lo que queremos. Sólo tenemos que ocuparnos del primer sumando.
Lo acotamos por
que a su vez está dominado por
En resumen, hemos sido capaces de demostrar que
La pregunta es ahora cómo obtener la estimación que buscamos, en
la que 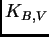 aparece con exponente 1.
aparece con exponente 1.
Lo primero es observar que en la definición de
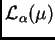 basta con tomar bolas ``
doblantes''. Una bola
basta con tomar bolas ``
doblantes''. Una bola 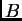 se dice que es
se dice que es
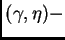 doblante, para
doblante, para 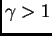 y
y
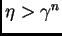 si
si
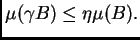 Es fácil ver, a partir de la condición
(
2.1), que para cualquier punto
Es fácil ver, a partir de la condición
(
2.1), que para cualquier punto 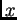 y cualquier
y cualquier 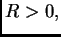 existe
alguna bola
existe
alguna bola
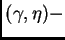 doblante centrada en
doblante centrada en 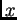 con radio
con radio
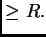 Asimismo, dado
Asimismo, dado 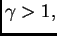 para
para 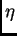 grande,
dependiendo de
grande,
dependiendo de 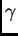 y
y 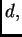 digamos
digamos
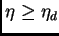 y para
y para
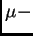 casi todo
casi todo
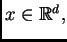 existe una sucesión de bolas
centradas en
existe una sucesión de bolas
centradas en 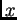 con radios que tienden a
con radios que tienden a 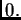 Para fijar ideas
llamaremos `` doblante'' sin más a toda bola
Para fijar ideas
llamaremos `` doblante'' sin más a toda bola
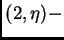 doblante, con
doblante, con
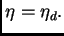 La suficiencia de la condición sobre bolas doblantes es un hecho
fundamental que fue observado por Tolsa para
La suficiencia de la condición sobre bolas doblantes es un hecho
fundamental que fue observado por Tolsa para
 La
demostración aquí es muy parecida. La segunda observación es el
siguiente lema, adaptado del correspondiente de Tolsa.
La
demostración aquí es muy parecida. La segunda observación es el
siguiente lema, adaptado del correspondiente de Tolsa.
Lema 7.3
Existe una constante
tal que si para un
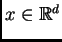
y cada
bola doblante
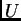
que contiene a
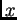
se tiene un número
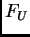
de
modo que
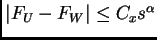
para cada par de bolas
doblantes
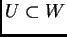
con
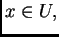
tales que
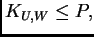
siendo
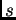
el radio de
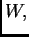
entonces
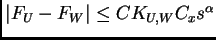
para cada par de bolas doblantes
con
siendo
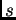
el radio de
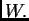
Con estas dos observaciones, vemos que nuestra estimación es
suficiente para probar el teorema.
Con las mismas técnicas se puede demostrar el siguiente resultado
Teorema 7.4
Sea
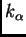
un núcleo fraccionario con regularidad
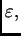
y
sean
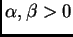
tales que
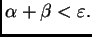
Entonces

es un operador acotado de
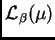
en
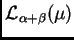
si y sólo
si
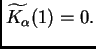



Next: Bibliography
Up: Operadores fraccionarios para medidas
Previous: El espacio `` regular''



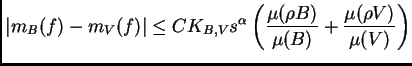
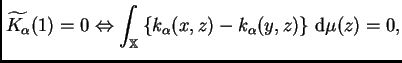
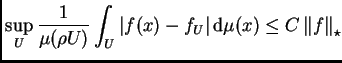
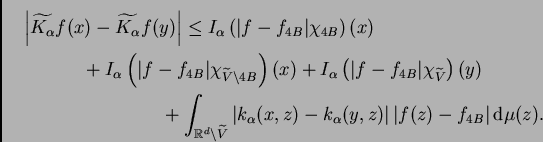
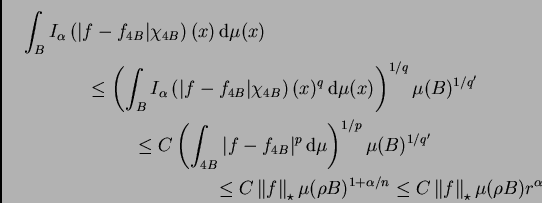
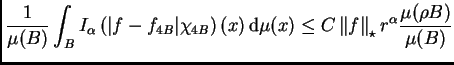
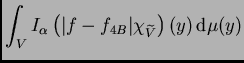
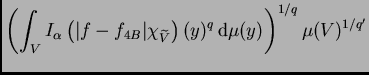
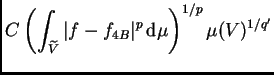
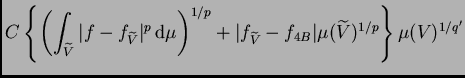
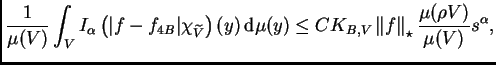
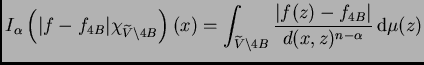
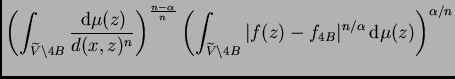
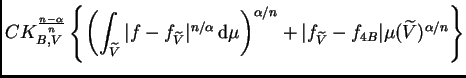
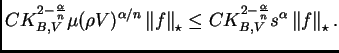
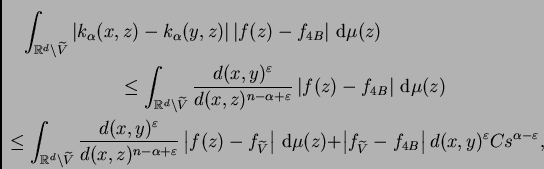
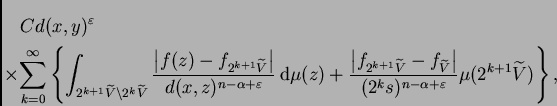
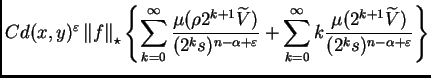
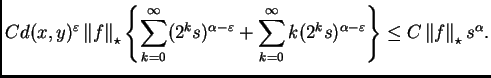
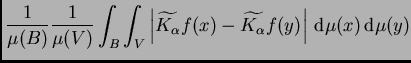
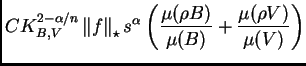
![]() basta con tomar bolas ``
doblantes''. Una bola
basta con tomar bolas ``
doblantes''. Una bola ![]() se dice que es
se dice que es
![]() doblante, para
doblante, para ![]() y
y
![]() si
si
![]() Es fácil ver, a partir de la condición
(
2.1), que para cualquier punto
Es fácil ver, a partir de la condición
(
2.1), que para cualquier punto ![]() y cualquier
y cualquier ![]() existe
alguna bola
existe
alguna bola
![]() doblante centrada en
doblante centrada en ![]() con radio
con radio
![]() Asimismo, dado
Asimismo, dado ![]() para
para ![]() grande,
dependiendo de
grande,
dependiendo de ![]() y
y ![]() digamos
digamos
![]() y para
y para
![]() casi todo
casi todo
![]() existe una sucesión de bolas
centradas en
existe una sucesión de bolas
centradas en ![]() con radios que tienden a
con radios que tienden a ![]() Para fijar ideas
llamaremos `` doblante'' sin más a toda bola
Para fijar ideas
llamaremos `` doblante'' sin más a toda bola
![]() doblante, con
doblante, con
![]() La suficiencia de la condición sobre bolas doblantes es un hecho
fundamental que fue observado por Tolsa para
La suficiencia de la condición sobre bolas doblantes es un hecho
fundamental que fue observado por Tolsa para
![]() La
demostración aquí es muy parecida. La segunda observación es el
siguiente lema, adaptado del correspondiente de Tolsa.
La
demostración aquí es muy parecida. La segunda observación es el
siguiente lema, adaptado del correspondiente de Tolsa.