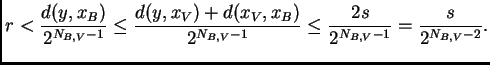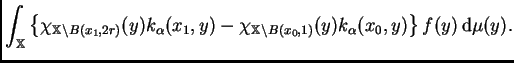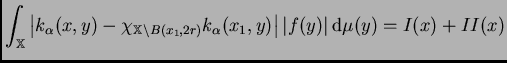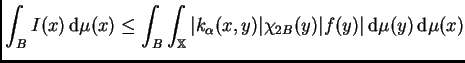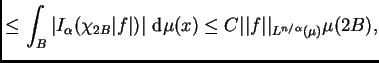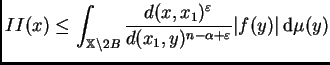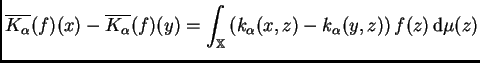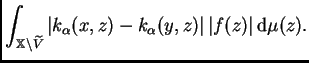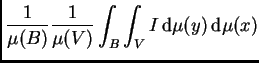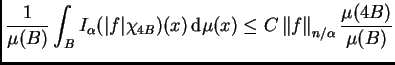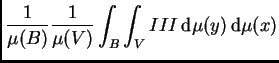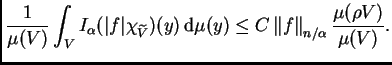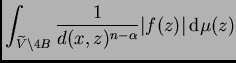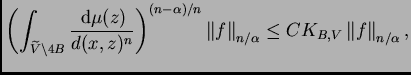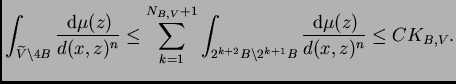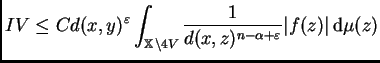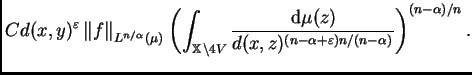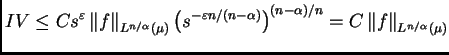Lema 6.3
Sean
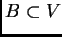
bolas.
Existe una constante
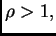
independiente de
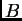
y
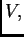
tal
que
donde
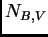
es el número entero que aparece en (6.3).
Demostración. Sean
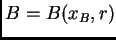 y
y
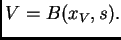 Entonces
Entonces
También, como
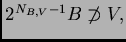
sabemos que existe
algún
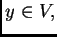
tal que
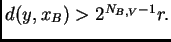
Por
consiguiente
Entonces si
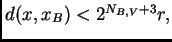
tenemos
que es lo que queríamos con
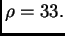
A partir de ahora y hasta el final de la sección usaremos el
valor fijo
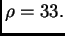
Definición 6.4
Sea
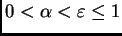
y supongamos que
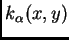
es un
núcleo fraccionario con regularidad
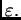
Para
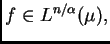
definimos
|
(6.5) |
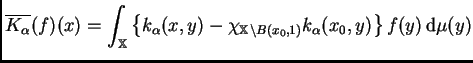 |
para algún
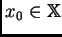
fijo. Veremos más abajo en el Teorema
6.5 que
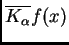
está bien definido
para casi todo punto
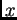
con respecto a
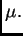
Aunque la definición depende de la elección de
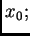
diferentes
elecciones de
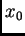
dan lugar a funciones que difieren solamente
en una constante.
Teorema 6.5
Sea
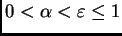
y supongamos que
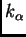
es como en
la última definición y
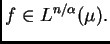
Entonces
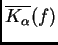
está bien definido por (
6.5) en
casi todo punto con respecto a
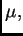
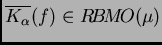
y
con
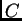
independiente de
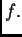
Demostración. Primero demostraremos la condición (
6.1) y, al mismo
tiempo, la existencia en casi todo punto de la integral en
(
6.5). Es suficiente demostrar que, para cada bola
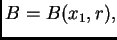
existe una constante
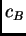
tal que
|
(6.6) |
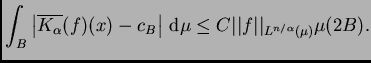 |
Tomemos
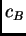
dada por
Claramente
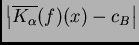
está dominado
por:
donde
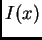
es la integral sobre

y
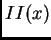
es la integral
sobre el complemento de
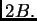
Estimamos a continuación las
integrales sobre
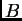
de
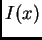
y
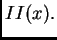
donde la última desigualdad es consecuencia del Lema
6.2. Para estimar la integral de
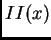
sobre
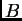
observamos primero
que, puesto que
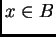
e
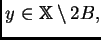
usando
(4.2) obtenemos
y, por la desigualdad de Hölder y el Lema
2.2 vemos que
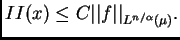
Por tanto, la integral de
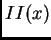
sobre
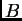
también está acotada por
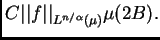
Ahora vamos a establecer
(
6.2). Sean
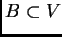
bolas,
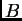
con radio
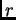
y
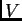
con radio
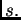
Veremos que
|
|
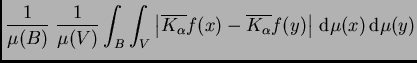 |
|
|
|
(6.7) |
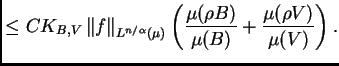 |
|
|
Observamos que el primer miembro de (
6.7) domina a
de modo que se obtiene (
6.2) para
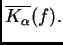
Sea
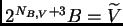
para la que sabemos por el
Lema
6.3, que
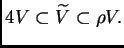
Para casi todos
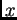
e
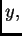
podemos escribir
Entonces
Denotemos por
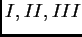
y
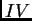
los cuatro términos del segundo
miembro de la última desigualdad. Estimamos separadamente la media
doble de cada uno de estos cuatro términos. El primero y el
tercero se tratan mediante el Lema
6.2 .
y, del mismo modo
Para tratar
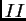
utilizamos la desigualdad de Hölder, obteniendo
pues
Finalmente, utilizando (
4.2)
Puesto que
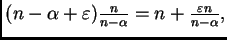
aplicando el Lema
2.2, obtenemos
lo que completa la demostración.


 Next: Espacios de Lipschitz ``
Up: Operadores fraccionarios para medidas
Previous: Espacios de Lipschitz
Next: Espacios de Lipschitz ``
Up: Operadores fraccionarios para medidas
Previous: Espacios de Lipschitz



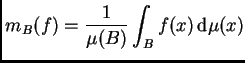 ; y también
; y también
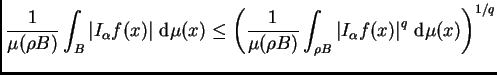
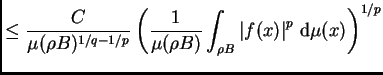
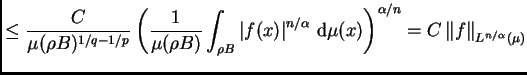
![]() y
y
![]() Entonces
Entonces