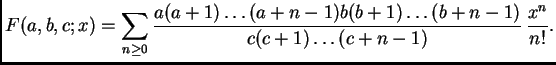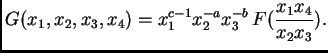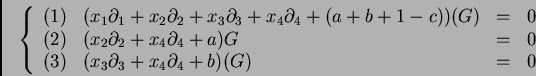Next: Los sistemas -hipergeométricos y
Up: Funciones hipergeométricas
Previous: Funciones hipergeométricas
La función hipergeométrica de Gauss como función
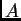 -hipergeométrica
-hipergeométrica
Dados 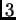 parámetros complejos
parámetros complejos 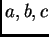 con
con
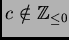 (o si
(o si
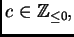 entonces
entonces
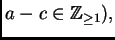 la función hipergeométrica
de Gauss
la función hipergeométrica
de Gauss
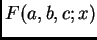 se define para
se define para 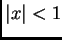 como
Por ejemplo,
como
Por ejemplo,
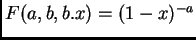 ,
,
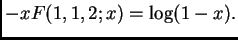 Es fácil verificar que
Es fácil verificar que
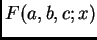 satisface
la ecuación diferencial lineal ordinaria
satisface
la ecuación diferencial lineal ordinaria
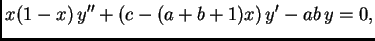 |
(3.1) |
y si llamamos
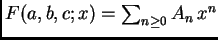 , el cociente
, el cociente
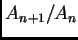 es una función
racional de
es una función
racional de 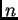 . La ecuación
(3.1) tiene tres puntos
singulares regulares en
. La ecuación
(3.1) tiene tres puntos
singulares regulares en 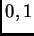 e
e 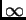 , y es, salvo normalización,
la forma general de una ecuación diferencial lineal ordinaria
de segundo orden con esta propiedad.
Podemos reformular esta ecuación diferencial en
, y es, salvo normalización,
la forma general de una ecuación diferencial lineal ordinaria
de segundo orden con esta propiedad.
Podemos reformular esta ecuación diferencial en 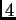 variables.
Dada una función univariada
variables.
Dada una función univariada 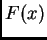 , llamemos
Entonces,
, llamemos
Entonces, 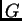 satisface las siguientes ecuaciones diferenciales lineales
parciales, que son simplemente versiones infinitesimales de condiciones
de homogeneidad:
Más aún,
satisface las siguientes ecuaciones diferenciales lineales
parciales, que son simplemente versiones infinitesimales de condiciones
de homogeneidad:
Más aún, 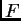 satisface la ecuación de Gauss (
3.1)
satisface la ecuación de Gauss (
3.1)
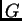 satisface la ecuación
satisface la ecuación
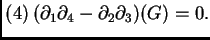 La ecuación de Gauss es equivalente al sistema
de ecuaciones lineales en derivadas parciales dado
por las cuatro ecuaciones
La ecuación de Gauss es equivalente al sistema
de ecuaciones lineales en derivadas parciales dado
por las cuatro ecuaciones
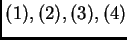 anteriores.
Este es el sistema
anteriores.
Este es el sistema 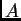 -hipergeométrico asociado
a la matriz entera
-hipergeométrico asociado
a la matriz entera
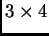 cuyas columnas están
dadas por los vectores
cuyas columnas están
dadas por los vectores
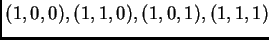 y al vector
y al vector
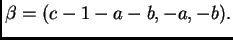



Next: Los sistemas -hipergeométricos y
Up: Funciones hipergeométricas
Previous: Funciones hipergeométricas