

Up: Funciones hipergeométricas
Previous: La función hipergeométrica de
En general, dado un subconjunto
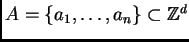 ,
consideramos la matriz (con igual nombre)
,
consideramos la matriz (con igual nombre)
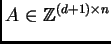 cuyas columnas
son los vectores
cuyas columnas
son los vectores
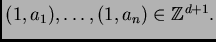 Para cada
vector
Para cada
vector
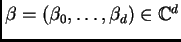 , el sistema
, el sistema
 -hipergeométrico con parámetro
-hipergeométrico con parámetro 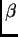 es el ideal
es el ideal
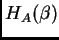 en el álgebra de Weyl en
en el álgebra de Weyl en 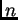 variables generado por los
operadores de Euler
variables generado por los
operadores de Euler
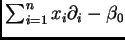 ,
y
,
y
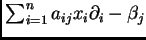 , para todo
, para todo
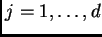 y por los siguientes operadores con
coeficientes constantes de
orden superior: para cada vector
y por los siguientes operadores con
coeficientes constantes de
orden superior: para cada vector
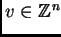 tal que
tal que
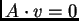 ,
escribamos
,
escribamos
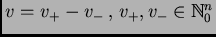 y consideremos
el operador
y consideremos
el operador
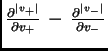 .
Decimos que una función holomorfa definida en un abierto
de
.
Decimos que una función holomorfa definida en un abierto
de
 es
es  -hipergeométrica (con parámetro
-hipergeométrica (con parámetro 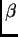 )
si es una solución del sistema de ecuaciones diferenciales en
)
si es una solución del sistema de ecuaciones diferenciales en 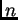 variables
definido por los operadores en
variables
definido por los operadores en
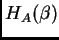 .
Este sistema es holónomo regular, y para vectores
.
Este sistema es holónomo regular, y para vectores
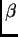 genéricos, su rango holonómico es el
volumen normalizado de la cápsula convexa de
genéricos, su rango holonómico es el
volumen normalizado de la cápsula convexa de  . El lugar
singular del sistema coincide con los ceros del discriminante
total
. El lugar
singular del sistema coincide con los ceros del discriminante
total
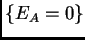 .
.
Ejemplo 3.1
Para el sistema equivalente al sistema de Gauss
que definimos en la sección §
3.1, el lugar singular
es la hipersuperficie definida por
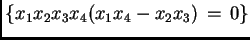
, y el rango holonómico, es decir la dimensión del
espacio de soluciones locales holomorfas en un punto
fuera del lugar singular, es igual a
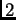
.
Un problema importante en este contexto es el estudio
de la monodromía de las funciones  -hipergeométricas.
Este es actualmente un problema abierto, del cual sólo
hay respuestas cuando la dimensión del núcleo de
-hipergeométricas.
Este es actualmente un problema abierto, del cual sólo
hay respuestas cuando la dimensión del núcleo de  es
es 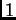 , que se reduce al caso clásico de una variable,
y para ciertos casos particulares en dos variables. En
particular, un problema es caracterizar las funciones
, que se reduce al caso clásico de una variable,
y para ciertos casos particulares en dos variables. En
particular, un problema es caracterizar las funciones
 -hipergeométrias invariantes por la monodromía,
es decir, estudiar las soluciones racionales de
-hipergeométrias invariantes por la monodromía,
es decir, estudiar las soluciones racionales de
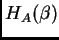 para
para 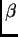 necesariamente entero (y resonante).
Dado que el lugar singular está descripto por los ceros
del discriminante total y en vista de la factorización
(
2.1), una función
necesariamente entero (y resonante).
Dado que el lugar singular está descripto por los ceros
del discriminante total y en vista de la factorización
(
2.1), una función  -hipergeométrica
racional tiene como denominador un producto de
ciertas potencias de
-hipergeométrica
racional tiene como denominador un producto de
ciertas potencias de 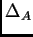 y de los discriminantes
de subconfiguraciones faciales de
y de los discriminantes
de subconfiguraciones faciales de  .
Tenemos el siguiente resultado [4]:
.
Tenemos el siguiente resultado [4]:
Teorema 3.2
Para configuraciones generales, el discriminante
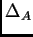
aparece en el denominador de una función

-hipergeométrica racional (para algún parámetro
entero
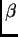
)
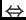

es la configuración de
Cayley asociada a una familia esencial
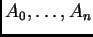
.
Por lo tanto, un

-discriminante aparece en el denominador
de una función

-hipergeométrica racional si y sólo
si el discriminante es de hecho una resultante
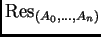
.
Más aún, todas las soluciones racionales que no son
polinomios de Laurent, se expresan en términos de residuos.
Por ejemplo, si consideramos el sistema  -hipergeométrico
asociado al polinomio univariado genérico de grado dos,
es decir al subconjunto
-hipergeométrico
asociado al polinomio univariado genérico de grado dos,
es decir al subconjunto
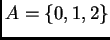 del ejemplo
1.1,
la función
del ejemplo
1.1,
la función
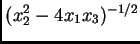 es
es  -hipergeométrica
(con parámetro
-hipergeométrica
(con parámetro 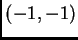 ), pero no existe ninguna solución
racional con polos en la variedad discriminantal
), pero no existe ninguna solución
racional con polos en la variedad discriminantal
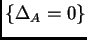 .
No hemos definido en esta breve exposición la noción
de configuración general que aparece en el enunciado
del Teorema
3.2, pero tiene un significado muy preciso
y alude a una propiedad que se verifica genéricamente.
El resultado es también cierto para todas las configuraciones
de dimensión uno, dos o tres, o de codimensión uno, y para las
configuraciones de Lawrence [3,4,5]. La conjetura es que el teorema
vale para cualquier configuración
.
No hemos definido en esta breve exposición la noción
de configuración general que aparece en el enunciado
del Teorema
3.2, pero tiene un significado muy preciso
y alude a una propiedad que se verifica genéricamente.
El resultado es también cierto para todas las configuraciones
de dimensión uno, dos o tres, o de codimensión uno, y para las
configuraciones de Lawrence [3,4,5]. La conjetura es que el teorema
vale para cualquier configuración  , y demostrarla completamente
es actualmente un problema abierto cuya solución
implicaría resolver sutiles problemas de clasificación geométrica
y problemas diofánticos.
, y demostrarla completamente
es actualmente un problema abierto cuya solución
implicaría resolver sutiles problemas de clasificación geométrica
y problemas diofánticos.
REFERENCIAS
[I] L. Blum, F. Cucker, M. Shub and S. Smale: Complexity and Real Computation, Springer, 1997.
[2] F. Catanese: Review of the book [10]. Bulletz'n AMS 37 (2) (2000) 183-198.
[3] E. Cattani, C. D'Andrea and A. Dickenstein: The Ahypergeometrie System Associated with a Monomial Curve, Duke J. Math. 99, N. 2, 179-207,1999.
[4] E. Cattani, A. Dickenstein and B. Sturmfels: Ratioiial Hyper-
geometric Functions. Compositio Mathematica 128 (2001) 217240.
[5] E. Cattani, A. Dickenstein and B. Sturmfels: Binomial Residues. Por aparecer: Annales de l'Instz'tut Fourier.
[6] D. Cox, J. Little and D. O'Shea: Using Algebraic Geometry. Springer, 1998.
[7] C. D' Andi-ea and A. Dickenstein: Explicit Formulas for the Multivariate Resultant. Proc. MEGA 2000, Journal of Pure and Applíed Algebra 164/1-2, 59-86, 2001.
[8] A. Dickenstein: Hypergeoinetric funetions with integer hornogeneities. Por aparecer: Proc. Meeting on Complex Analysis (June -July 1998), Eds. F. Norguet and S. Ofman, International Press.
[9] A. Dickenstein and B. Sturmfels: Elimination Theory in Codimension Two. Preprint 294, Instituto Argentino de Matemática y FCEYN, Dto. de Matemática, UBA, 2001.
[10] I. M. Gel'fand, M. Kapranov and A. Zelevinsky: Discriminants, Resultants and Multidimensional Determinants, Birkháuser, Boston, 1994.
[11] I. M. Gel'fand, A. Zelevinsky and M. Kapranov: Hypergeometrie Functions and Toral Manifolds. Functz'onal Analysz's and z'ts Appl. 23 (1989) 94-106.
[12] l. M. Gel'fand, M. Kapranov and A. Zelevinsky: Newtoil Polytopes of the Classical Discriminant and Resultant. Advaínceg in Math. 84 (1990) 237-254.
[13] I. M. Gel'fand, A. Zelevinsky and M. Kapranov: Discriminants
of Polynomials in Several Variables and Triangulations of Newton Polytopes. Leningrad Math. J. 2 (1991) 449-505.
[14] B. Sturmfels: Sparse Elimination Theory. In Computational Algebraic Geometry and Commutative Algebra (D. Eiseilbud, L. Robbiano, eds.), Proceedings, Cortona, June 1991. Cambridge University Press, 1993.
[15] B. Sturmfels, On the Newton polytope of the resultant, Journal of Algebraic Combinatorícs 3 (1994) 207-236.
[16] M. Saito, B. Sturmfels, and N. Takayama: Grübner Deformations of Hypergeometric Differential Equations, Algorithms and Computation in Mathematics, Volume 6, Springer-Verlag, Heidelberg, 2000.
[17] T. M. Sadykov: The Hadamard Product of Hypergeometric Series. Preprint, U. Stockholm, 2001.


Up: Funciones hipergeométricas
Previous: La función hipergeométrica de
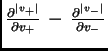 .
Decimos que una función holomorfa definida en un abierto
de
.
Decimos que una función holomorfa definida en un abierto
de